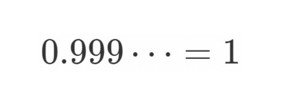同じはずが違う。違うはずが同じ。

店長ブログ

同じはずが違う。違うはずが同じ。

スタッフ 2025/10/25 06:06

「1」と「0.99999...」は違う数字なのに同じ数字らしい。（？）

1/3（さんぶんのいち）＝0.33333...

左右どちらの式にも同じ値を掛けても同じになるので

（1/3）×3　（さんぶんのいちかけるさん）　＝　0.33333...×3

すなわち

1　＝　0.99999...

違うやり方で考えてみました。
まず
xを0.99999...と仮定します。

x　＝　0.99999...

左右の式、どちらも10倍にします。

10x　＝　9.99999...

左右の式どちらも「x」を引きます。

10x　ー　x　＝　9.99999...　ー　0.99999...

計算すると

9x　＝　9

左右の式、どちらも9で割ると「x」の答えが出ます。

x　＝　1

なぜか「0.99999...」だったのに「1」になってしまいました。

どの式もおかしくないのに答えはおかしくなってしまう。
なんででしょうか・・・・？
数学？って難しいですね！(>_<)

お問い合わせ

電話:080-6264-3131 LINE　ID:mdm-style メール:m-d-m3131@ezweb.ne.jp

スマホからボタンをタップで簡単にお問合せができます。

求人情報を見る｜お店サイトを見る｜女の子達のプライベート日記を見る

プロフィール

ニックネーム：Sunrise Group　～マダムスタイル～　ジャマイカ店長（日本人です）
SUNRISE GROUP　ジャマイカ（日本人）です。

働く女性を第一に考えに考えて今までやってきました。
SUNRISE GROUPです。
これからももちろん働いてくれる女性の事を第一というのは
変わることはありません。

マダムスタイルもできてはや数年、
最近は出戻りされる女性が増えてきました。
「他のお店に行ってみたけど、やっぱりここが良かったです。」
「やっぱり厳しくなってこの業界に戻ろうと思ったときにここしか考えなかったです。」
とても嬉しいですね。

当店、当グループを辞める女性は全員

「この業界からの卒業」

となれるお店・グループ作りを頑張っていきたいと思います。

お店データ

◇店名
マダムスタイル(サンライズグループ)
◇職種
人妻デリヘル
◇勤務エリア
岡山

求人情報を見る
サイトを見る

日	月	火	水	木	金	土
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

店舗名	マダムスタイル(サンライズグループ)
内容【必須】	下記より該当項目にチェックを入れて下さい。お店がやっていない（閉店している）お店の名前が違う応募用電話番号が違う（繋がらない）応募用メールアドレスが違う（エラーになる）実際のお仕事内容・待遇がガールズヘブンの記載と違うオフィシャルHPのURLが違う（繋がらない）その他
連絡先	ご提供内容の確認をさせて頂くことが発生した際にのみ使用致します
詳細

マダムスタイル(サンライズグループ)

先輩ボイス

店長ブログ

同じはずが違う。違うはずが同じ。

プロフィール

お店データ

最新のブログ一覧

カレンダー

アーカイブ

編集部に通報

マダムスタイル(サンライズグループ)

先輩ボイス

店長ブログ

同じはずが違う。違うはずが同じ。

プロフィール

お店データ

最新のブログ一覧

カレンダー

アーカイブ

SNS応募方法

編集部に通報